Задача: На плоскости координатами своих вершин задан треугольник. Определить, к какому типу он принадлежит (остро- , тупо- или прямоугольный)
Const
eps = 10E-5;
{
Поскольку в стандартной библиотеке Паскаля функция вычисления арккосинуса
отсутствует, пишем ее самостоятельно ...
}
Function ArcCos(X: Double): Double;
Begin
If abs(X) < eps Then arccos := Pi / 2
Else
arccos := ArcTan(Sqrt(1 - Sqr(X)) / X) + Pi * Byte(X < 0);
End;
Type
{ Структура для хранения координат X, Y точки }
Point = Record
X, Y: double;
End;
Const
{ Переменная для хранения признака того, что один из углов треугольника - прямой ... }
is90: Boolean = False;
{
Процедура, запрашивающая у пользователя ввод координат X и Y определенной точки,
и возвращающая эту точку через Var-параметр...
}
Procedure GetCoord(Const s: string; Var P: Point);
Begin
WriteLn('Point ' + s);
Write('X = '); ReadLn(P.X);
Write('Y = '); ReadLn(P.Y);
End;
{
Функция для определения расстояния между двумя точками ...
(Зачем нужен Var-параметр dist - см. комментарии после программы)
}
Function GetDist(Var dist: Double; pA, pB: Point): Double;
Begin
dist := Sqrt(Sqr(pA.X - pB.X) + Sqr(pA.Y - pB.Y));
GetDist := dist;
End;
{
Функция, возвращающая угол (в градусах !!!) между двумя сторонами
треугольника, вычисленный из формулы теоремы косинусов
}
Function Angle(A, B, C: Double): Double;
Var value: Double;
begin
Value := ArcCos((Sqr(A) + Sqr(B) - Sqr(C)) / (2 * A * B)) * (180 / Pi);
If Abs(value - 90) < eps Then is90 := True;
Angle := value;
End;
Var
{
Переменные для хранения вершин треугольника
}
pA, pB, pC: Point;
{
Длины сторон треугольника:
A - длина стороны AB;
B - длина стороны BC;
C - длина стороны AC;
}
A, B, C: double;
{
Углы треугольника:
alpha - угол между AC и BC (противолежит AB)
beta - угол между AB и AC (противолежит BC)
gamma - угол между AB и BC (противолежит AC)
}
alpha, beta, gamma: double;
begin
{
Получаем координаты вершин треугольника
}
GetCoord('A', pA);
GetCoord('B', pB);
GetCoord('C', pC);
{
Вычисляем все углы в заданном треугольнике
}
alpha := Angle(
GetDist(B, pB, pC),
GetDist(C, pA, pC),
GetDist(A, pA, pB)
);
beta := Angle(A, C, B);
gamma := Angle(A, B, C);
{
И по вычисленным углам делаем вывод о том,
является ли данный треугольник остро- , тупо- или прямоугольным
}
If is90 Then WriteLn('Прямоугольный')
Else
If (alpha < 90) and (beta < 90) and (gamma < 90) then WriteLn('Остроугольный')
Else
If (alpha > 90) or (beta > 90) or (gamma > 90) then WriteLn('Тупоугольный')
end.
А теперь немного о том, зачем в функции GetDist понадобился еще один параметр...... A := GetDist(pA, pB); B := GetDist(pB, pC); C := GetDist(pA, pC); alpha := Angle(B, C, A); beta := Angle(A, C, B); gamma := Angle(A, B, C); ...Введением же одного дополнительного параметра я добился того, что одновременно с вычислением всех длин сторон найденные значения подставляются в первый вызов функции Angle (получилось нечто вроде C-шного:
alpha = Angle(
(B = GetDist(pB, pC)),
(C = GetDist(pA, pC)),
(A = GetDist(pA, pB))
);
, только средствами Паскаля. Иногда это действительно удобно)Задача: Определение принадлежности точки к многоугольнику
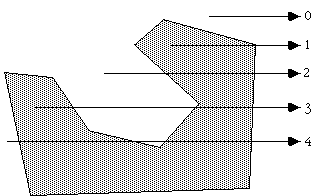
Ниже приведено простое решение проблемы, часто встречающейся в компьютерной графике, определение, лежит ли
точка (x,y) внутри или снаружи двумерного многоугольника. В частности, это может быть необходимо в задачах определяющих
пересечение нескольких полигонов.
Будем считать, что многоугольник состоит из N вершин (xi, yi) где i изменяется от 0 до N-1.
Последняя вершина (xN,yN) считается равной первой вершине (x0,y0),
то есть, многоугольник замкнут. Для того, чтобы определить положение точки (xp,yp),
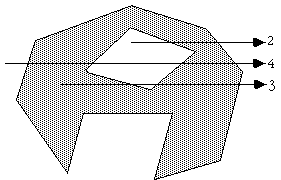
представим горизонтельный луч, выходящий из (xp,yp), и уходящий вправо. Если количество
пересечений этого луча с отрезками, формирующими многоугольник, является четным, то точка лежит вне многоугольника.
Если же число пересечений нечетно, то точка (xp,yp) лежит внутри многоугольника. См. рисунок:

Uses Crt;
Function min(a, b: Double): Double;
Begin
min := a;
If b < a Then min := b;
End;
Function max(a, b: Double): Double;
Begin
max := a;
If b > a Then max := b;
End;
{
Структура, описываюшая тип точки
}
Type
Point = Record
x, y: Double;
End;
Function InsidePolygon(Var polygon: Array Of Point;
Const n: Integer; p: Point): Boolean;
Var
i, counter: Integer;
xinters : Double;
p1, p2 : Point;
Begin
counter := 0;
p1 := polygon[0];
For i := 1 To n Do Begin
p2 := polygon[i mod n];
If p.y > min(p1.y, p2.y) Then Begin
If p.y <= max(p1.y, p2.y) Then Begin
If p.x <= max(p1.x, p2.x) Then Begin
If p1.y <> p2.y Then Begin
xInters := (p.y - p1.y)*(p2.x - p1.x) / (p2.y-p1.y) + p1.x;
If (p1.x = p2.x) or (p.x <= xInters) Then Inc(counter);
End;
End;
End;
End;
p1 := p2;
End;
If (counter mod 2) = 0 Then InsidePolygon := False
Else InsidePolygon := True;
End;
Const
{ Максимально возможное количество вершин полигона }
maxPoints = 24;
Var
P : Point; { Проверяемая точка }
Poly: Array[0 .. 24] of Point; { Массив вершин многоугольника }
{
Функция ввода данных (возвращает количество точек, образующих полигон)
Внимание !!! Порядок ввода точек, образующих многоугольник - против часовой стрелки...
}
Function EnterData: Integer;
Var
i, count: integer;
Begin
Write('Enter poly`s vertex number: '); ReadLn(count);
For i := 0 To Pred(count) Do Begin
Write('X[',i,']: '); ReadLn(Poly[i].x);
Write('Y[',i,']: '); ReadLn(Poly[i].y);
End;
WriteLn;
Write('Point X: '); ReadLn(P.x);
Write('Point Y: '); ReadLn(P.y);
End;
Var
count: Integer; { Количество точек в многоугольнике }
Begin
ClrScr;
count := EnterData;
WriteLn;
If InsidePolygon(Poly, count, P) Then
WriteLn('Точка внутри многоугольника')
Else
WriteLn('Точка ВНЕ многоугольника');
ReadLn;
End.
Задача:
В строке данных записаны 30 чисел от 1 до 8, показывающих, в каком направлении дул ветер в соответствующий день месяца
(1-северный, 2-северо-восточный, 3-восточный, 4-юго-воточный, 5 южный, 6-юго-западный, 7-западный, 8-северо-западный).
Вывести на экран “розу ветров” - многоугольник, вершинами которого лежат на 8-лучах, выходящих из общего центра с равным углами,
расстояния от вершины до этого центра пропорционально дней месяца, в который дул соответствующий ветер.
Для отображения результата данной задачи идеально подходит полярная система координат: лучи выходят из общего центра, на них
нужно откладывать расстояние, пропорциональное количеству... неважно чего, главное - что на них...
Вот как решается данная задача (есть вопросы по решению - задаем сюда: Форум "Интересные задачи для программистов"):
uses graph;
type
Dir = (
E, NE, N, NW, W, SW, S, SE
);
arrType = array[Dir] of integer;
const
titles: array[Dir] of string = (
'E', 'NE', 'N', 'NW', 'W', 'SW', 'S', 'SE'
);
start = ord(low(Dir));
finish = ord(high(dir));
amount = finish - start + 1;
sector = (360 div amount) * (Pi / 180);
function read_data(var arr: arrType): integer;
var
i, X, max: integer;
ix: Dir;
begin
for ix := low(Dir) to
high(Dir) do arr[ix] := 0;
for i := 1 to 30 do begin
read(X);
if X <= 3 then X := 4 - X else X := 12 - X;
inc(arr[Dir(pred(X))]);
end;
max := 0;
for ix := low(Dir) to high(Dir) do
if arr[ix] > max then max := arr[ix];
read_data := max;
readln;
end;
var
center_x, center_y: integer;
const
mult = 20;
function get_x(r, phi: real): integer;
begin
get_x := center_x + trunc(mult * r * cos(phi));
end;
function get_y(r, phi: real): integer;
begin
get_y := center_y - trunc(mult * r * sin(phi));
end;
procedure line_polar(phi_st, r_st, phi_fn, r_fn: real);
begin
line(
get_x(r_st, phi_st), get_y(r_st, phi_st),
get_x(r_fn, phi_fn), get_y(r_fn, phi_fn)
);
end;
procedure text_polar(phi, r: real; const T: string);
begin
outtextxy(
get_x(r, phi), get_y(r, phi), T
);
end;
procedure circle_polar(phi, r: real; radius: integer);
begin
circle(
get_x(r, phi), get_y(r, phi), mult * radius
);
end;
var
arr: arrType;
i, j,
max_val: integer;
{
Это - только для того, чтобы программа запускалась как на Турбо, так и на Free-Паскале...
}
gDriver, gMode, errCode:
{$ifdef FPC}
smallint
{$else}
integer
{$endif}
;
begin
max_val := read_data(arr);
initgraph(gDriver, gMode, '');
errCode := graphresult;
if errCode <> grOk then begin
writeln('error: ', grapherrormsg(errCode));
readln; halt(100);
end;
center_x := getmaxx div 2;
center_y := getmaxy div 2;
for i := start to finish do begin
setcolor(white);
line_polar(0, 0, i * sector, 10);
text_polar(i * sector, 11, titles[Dir(i)]);
if i = finish then j := start else j := i + 1;
setcolor(red);
line_polar(i * sector, arr[Dir(i)], j * sector, arr[Dir(j)])
end;
setcolor(darkgray);
for i := 1 to max_val do
circle_polar(0, 0, i);
readln;
closegraph;
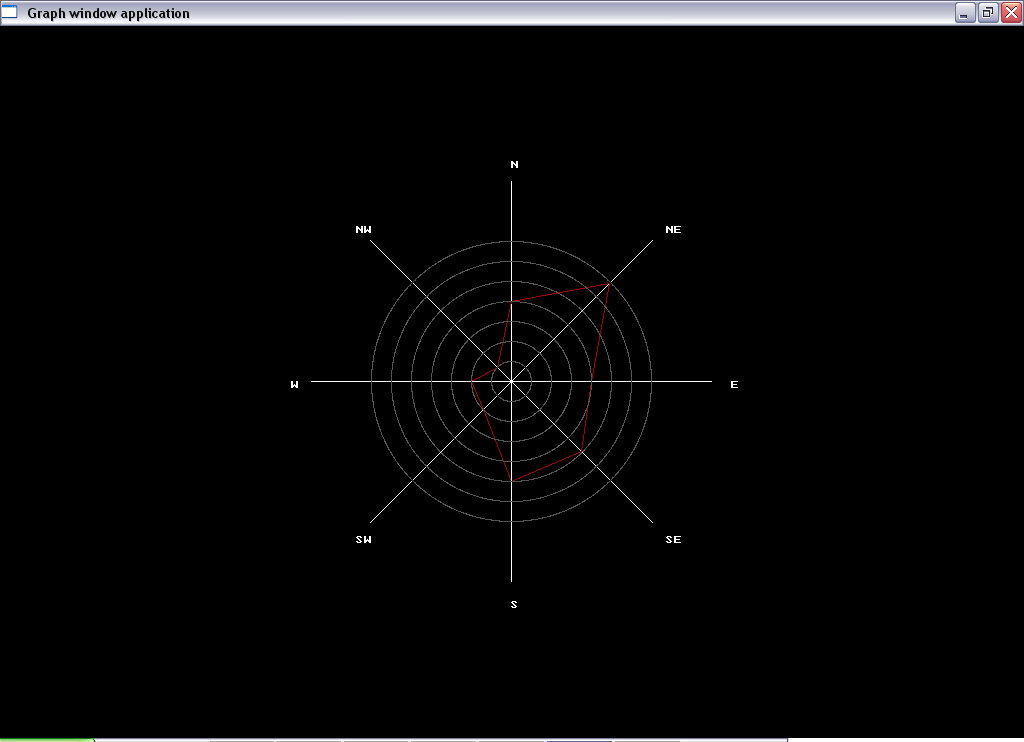
end.После компиляции и запуска этой программы вводим массив чисел (я вводил такой:
1 2 3 4 5 6 7 8 1 2 2 2 2 3 4 5 5 4 2 6 5 5 3 4 7 1 1 2 3 4), получаем вот такую "Розу ветров" (нажмите на картинку для ее увеличения):
Задача: Написание программы для создания и проведения тестов.
Программа должна уметь работать с вопросами нескольких типов:
{ максимально возможное количество ответов на вопрос ... }
const
max_answers = 10;
type
{ здесь описываем 5 типов ответов, каждый из них будет обрабатываться по-своему }
QuestType = (ans1, ans2, ans3, ans4, ans5);
{ промежуточная структура, для хранения соответствий между двумя вариантами - для 4-го типа }
TS = record
first, second: integer;
end;
{ это - сама запись с вариантами... }
TTest = record
quest: string[50];
ans_count: 0 .. max_answers;
answers: array[1 .. max_answers] of string[50];
case qType: QuestType of
ans1: (
good_ans1: string[50];
);
ans2: (
good_ans2: integer;
);
ans3: (
good_count3: 1 .. max_answers;
good_ans3: array[1 .. max_answers] of integer;
);
ans4: (
good_count4: 0 .. max_answers;
good_ans4: array[1 .. max_answers] of TS;
);
ans5: (
good_ans5: array[1 .. max_answers] of integer;
);
end;
Основная сложность возникает при обработке первого типа вопросов: как заставить программу понимать, что и "Л. Н. Толстой" и "Лев Толстой",
и даже "Толстой Л. Н." являются правильными ответами.{
Тип данных для разбиения строки на слова
}
type
TWordStr = string[100];
TDelimiter = set of Char;
PTItem = ^TItem;
TItem = record
Data: TWordStr;
next: PTItem;
end;
TWordList = record
first, last: PTItem;
end;
{
Процедура, помещающее очередное найденное слово в список
}
procedure InsertWord(var L: TWordList; s: string);
var p: PTItem;
begin
New(p);
p^.Data := s;
p^.next := nil;
if L.first = nil then L.first := p
else L.last^.next := p;
L.last := p
end;
{
Собственно процедура разбиения на слова
}
function GetWords(s: string; var L: TWordList; delimiters: TDelimiter): Byte;
var i, p: Byte;
begin
for i := 1 to Length(s) do
if s[i] In delimiters then s[i] := #32;
repeat
p := Pos(' ', s);
if p > 0 then Delete(s, p, 1)
until p = 0;
if s[1] = ' ' then Delete(s, 1, 1);
if s[Length(s)] = ' ' then Delete(s, Length(s), 1);
i := 0;
repeat
p := Pos(' ', s); Inc(i);
if p > 0 then begin
InsertWord(L, Copy(s, 1, Pred(p)));
Delete(s, 1, p)
end
else InsertWord(L, s)
until p = 0;
GetWords := i
end;
const
{ Максимально допустимое число ответов на вопрос }
max_answers = 10;
type
{ Типы вопросов - выделены в отдельное перечисление для структуризации программы }
QuestType = (ans1, ans2, ans3, ans4, ans5);
{ Тип - "пара значений", для вопросов 4-ой группы }
TS = record
first, second: integer;
end;
{ Запись с вариантами - основная структура, используемая в программе }
TTest = record
{ Сам вопрос, на который предстоит ответить тестируемому }
quest: string[50];
{ Количество вариантов ответа на вопрос }
ans_count: 0 .. max_answers;
{ Собственно, варианты ответа на вопрос }
answers: array[1 .. max_answers] of string[50];
case qType: QuestType of
{ тип №1: непосредственный ввод - Храним шаблонную строку ответа }
ans1: (
good_ans1: string[50];
);
{
тип №2: один правильный из нескольких.
Храним индекс правильного ответа
}
ans2: (
good_ans2: integer;
);
{
тип №3: несколько правильных из нескольких.
Храним массив индексов правильных ответов и их число
}
ans3: (
good_count3: 0 .. max_answers;
good_ans3: array[1 .. max_answers] of integer;
);
{
тип №4: вопросы на соответствие.
Храним массив правильных соответствий индексов
}
ans4: (
good_count4: 1 .. max_answers;
good_ans4: array[1 .. max_answers] of TS;
);
{
тип №5: вопросы на сортировку.
Храним индексы в правильно отсортированном виде
}
ans5: (
good_ans5: array[1 .. max_answers] of integer;
);
end;
{ Заодно описываем и тип файла для хранения подобных записей }
TestFile = file of TTest;
const
{ сообщения для пользователя - для разгрузки текста программы выделены в отдельный массив }
msg: array[QuestType] of string = (
'type #1 - enter the answer: ',
'type #2 - enter the good answer index: ',
'type #3 - enter the good answer index: ',
'type #4 - enter the pairs (first - second): ',
'type #5 - enter the good-sorted indexes: '
);
{
Процедура, запрашивающая у составителя теста вопрос, и заполняющая запись R
всеми данными, необходимыми для правильной обработки ответа на него
}
procedure get_quest(var R: TTest);
{
Вспомогательная функция - получение от пользователя целого числа в заданном интервале
}
function get_integer(const title: string;
range_start, range_finish: integer): integer;
var X: integer;
begin
write(title + '[', range_start, ' .. ', range_finish, '] ');
repeat
readln(X);
until (X >= range_start) and (X <= range_finish);
get_integer := X;
end;
var
i, X: integer;
begin
{ Для любого типа вопросов небоходимо ввести сам вопрос }
write('question: '); readln(R.quest);
{ Теперь запросим у составителя, какой тип у этого вопроса и приведем его к QuestType }
R.qType := QuestType(get_integer('test', 1, 5) - 1);
{ В зависимости от того, к какому типу относится вопрос, его обработка осуществляется по-разному }
case R.qType of
{ тип №1 - количество правильных ответов не нужно, вводится только шаблонный ответ }
ans1:
begin
R.ans_count := 0;
write(msg[ans1]); readln(R.good_ans1);
end;
{ Все остальные типы: запрашивается количество вариантов ответа, и затем - сами варианты }
ans2 .. ans5:
begin
R.ans_count := get_integer('answers count', 1, max_answers);
for i := 1 to R.ans_count do begin
write('answer #', i:2, '':2); readln(R.answers[i]);
end;
{
Запрос правильных ответов необходим только для этих типов вопросов,
но не для первого, поэтому информационная строка печатается здесь,
а не в основном теле процедуры
}
writeln('good answers:');
end;
end; { Case }
{
Теперь переходим ко вводу правильных ответов.
Также в зависимости от выбранного типа вопроса
}
case R.qType of
{ Тип №2: вводим один индекс правильного ответа }
ans2:
begin
R.good_ans2 := get_integer(msg[ans2], 1, R.ans_count);
end;
{ Тип №3: вводим несколько (пока не будет введен 0) индексов правильных ответов }
ans3:
begin
R.good_count3 := 0;
i := 1;
repeat
X := get_integer(msg[ans3] + ' (0 to finish) ', 0, R.ans_count);
{ Что-то было введено, кроме 0 - дописать это в массив ответов }
if X <> 0 then begin
R.good_ans3[i] := X;
inc(R.good_count3);
inc(i);
end;
until X = 0; { Ввели 0 - надо выходить из цикла }
end;
{ Тип №4: ввод пар соответствий }
ans4:
begin
write(msg[ans4]);
for i := 1 to R.ans_count do begin
R.good_ans4[i].first := get_integer('first', 1, R.ans_count);
R.good_ans4[i].second := get_integer('second', 1, R.ans_count);
end;
end;
{ Тип №5: ввод правильно отсортированной последовательности индексов }
ans5:
begin
write(msg[ans5]);
for i := 1 to R.ans_count do begin
write('will be #', i);
R.good_ans5[i] := get_integer('', 1, R.ans_count);
end;
end;
end; { Case }
end;
{
Функция получает из основной программы структуру R с вопросом, прочитанную из файла,
задает пользователю записанный в структуре вопрос, в соответствии с типом вопроса
запрашивает ответ.
Возвращает True в случае, если ответ совпадает с записанным в R; иначе возвращает False
}
function get_answer(const R: TTest): boolean;
{
Дополнительная процедура: вывод на экран всех вариантов ответа на вопрос
}
procedure print_options;
var i: integer;
begin
for i := 1 to R.ans_count do begin
write(i:2, ') ', R.answers[i] + ' ');
end;
end;
var
{ Для типа №1 }
s: string;
L: TWordList;
p: ptitem;
count, positive, negative: integer;
{ Для типа №2 }
i, choice: integer;
{ Для типа №4 }
pair: TS;
j: integer;
begin
{ Вывод сообщения о типе вопроса, и самого текста вопроса }
writeln(msg[R.qType]);
writeln(R.quest);
{ Обработка будет различной в зависимости от типа }
case R.qType of
{
Тип №1: запрашваем у отвечающего строку, разбиваем ее на слова,
и проверяем наличие каждого слова в шаблонной строке, хранящейся в R...
Если число совпадений больше числа НЕсовпадений, то считаем ответ правильным
}
ans1:
begin
readln(s);
L.first := nil;
count := GetWords(s, L, [#32]);
{ Начинаем проход по списку слов }
p := L.first;
positive := 0; negative := 0;
while p <> nil do begin
if pos(p^.Data, R.good_ans1) > 0 then inc(positive)
else inc(negative);
p := p^.next;
end;
get_answer := (positive > negative);
end;
{
Тип №2: выводим варианты ответов, и запрашиваем ввод
одного индекса. Если он совпадает с тем, что хранится в R
как правильный, то ответ засчитывается, иначе - нет
}
ans2:
begin
print_options;
writeln;
write('your choice: '); readln(choice);
get_answer := (choice = R.good_ans2);
end;
{
Тип №3: Выводим варианты ответов, и запрашиваем ввод одного индекса.
После чего проверяем, содержится ли он в массиве индексов, помеченных
как правильные (R.good_ans3). Если да - ответ засчитывается
}
ans3:
begin
print_options;
writeln;
write('your choice: '); readln(choice);
get_answer := false;
for i := 1 to R.good_count3 do
if choice = R.good_ans3[i] then get_answer := true;
end;
{
Тип №4: Вывод вариантов ответов и запрос пользователю:
"введи правильные соответствия между элементами первого
и второго столбцов". Если в массиве правильных ответов содержатся
ВСЕ такие же соответствия (причем в любой последовательности,
порядок не важен) - то ответ засчитывается.
}
ans4:
begin
print_options;
writeln;
writeln('answer:');
count := 0;
for i := 1 to R.ans_count do begin
write('C1) '); readln(pair.first);
write('C2) '); readln(pair.second);
for j := 1 to R.ans_count do begin
if
(R.good_ans4[j].first = pair.first) and
(R.good_ans4[j].second = pair.second)
then inc(count);
end;
end;
get_answer := (count = R.ans_count);
end;
{
Тип №5: выводим варианты ответа, и запрашиваем ввод индексов
в правильном порядке. Если ВСЕ введенные индексы совпадают с
соответствующими элементами массива правильных индексов,
то ответ засчитывается
}
ans5:
begin
print_options;
writeln;
writeln('answer (sorted index array)');
get_answer := true;
for i := 1 to R.ans_count do begin
write('-> '); readln(choice);
if choice <> R.good_ans5[i] then get_answer := false;
end;
end;
end; { Case }
end;
var
Rec: TTest;
F: TestFile;
i, n: integer;
b: boolean;
begin
assign(F, 'quest.dat');
{$i-}
reset(F);
{$i+}
if ioResult <> 0 then begin
rewrite(F);
write('questions to enter: '); readln(n);
for i := 1 to n do begin
get_quest(Rec);
write(F, Rec);
end;
reset(F);
end
else begin
while not eof(F) do begin
read(F, Rec);
b := get_answer(Rec);
writeln('result = ', b);
end;
end;
close(F);
end.
"Звездное небо" (ООП-реализация):
Скачать программу можно отсюда:
starf.rar
Новогодняя елка + снегопад (версия для FPC начиная с 2.2.0):
Скачать программу можно отсюда:
elka_fpc.zip
Решение уравнений различных степеней:
Очень часто при решении задач необходимо находить корни уравнений различных порядков (квадратных, кубических и т.д.)
Вместо того, чтобы писать свое решение этой задачи, можно воспользоваться функциями, которые содержатся в присоединенном
модуле Equation:
Function solveQuadratic(Var x, y: Array Of Double): Byte;Решение квадратного уравнения вида: x[0] * x[sup]2[/sup] + x[1] * x + x[2] = 0
{$n+}
Uses Equation;
Const
ax: Array[0 .. 2] Of Double =
(24, -50, 25 );
Var
ay: array[0 .. 2] Of Float;
roots, i: Integer;
Begin
roots := solveQuadratic(ax, ay);
Writeln( 'number of roots = ', roots );
For i := 0 To Pred(roots) Do
WriteLn( 'root #', i + 1, ' = ', ay[ i ] :10 :5 );
End.
Function solveCubic(Var x, y: Array Of Double): Byte;Решение кубического уравнения: x[0] * x[sup]3[/sup] + x[1] * x[sup]2[/sup] + x[2] * x + x[3] = 0
{$n+}
Uses Equation;
Const
ax: Array[0 .. 3] Of Float =
(1, 0, -9, 4 );
Var
ay: array[0 .. 3] Of Float;
roots, i: Integer;
Begin
roots := solveCubic(ax, ay);
Writeln( 'number of roots = ', roots );
For i := 0 To Pred(roots) Do
WriteLn( 'root #', i + 1, ' = ', ay[ i ] :10 :5 );
End.
Function solveQuarticAlgebra(Var x, results: Array Of Double): Byte;
Function solveQuarticVieta(Var x, results: Array Of Double): Byte;
Function PolySolve(Const order: Integer;
Var coeffs, roots: Array Of Double): Integer;
, позволяющая решать алгебраические уравнения практически любого порядка (порядок задается константой maxOrder,
и изначально установлен равным 12) при помощи последовательности Штурма.{$n+}
Uses Equation;
Const
Order = 4;
coeffs: Array[0 .. Order] Of Double = (
1, 0, -25, 60, -36
);
Var
roots: array[0 .. maxOrder] Of Double;
nroots, i: Integer;
begin
WriteLn('Vieta method :');
nroots := solveQuarticVieta(coeffs, roots);
{ nroots := solveQuarticAlgebra(coeffs, roots); }
Writeln( 'number of roots = ', nroots );
For i := 0 To Pred(nroots) Do
WriteLn( 'root #', i + 1, ' = ', roots[ i ] :7 :4 );
WriteLn;
WriteLn('Sturm sequence method :');
nroots := PolySolve(Order, coeffs, roots);
If nroots = 0 Then Begin
WriteLn('solve: no real roots'); Halt(0)
End
Else Begin
WriteLn(nroots, ' distinct real root(s) for x: ');
For i := 0 To Pred(nroots) Do
WriteLn('root #', i + 1, ' = ', roots[ i ] :7 :4);
End;
end.
Сам модуль можно взять здесь: equation.pasЗадача: Построить таблицу истинности логического выражения.
{
Функция, переводящая десятичное число в другую систему счисления
}
function fromdec(n, radix: longint): string;
var s: string;
const
digit: string[16] = '0123456789ABCDEF';
begin
s := '';
repeat
s := digit[(n mod radix) + 1] + s;
n := n div radix;
until n = 0;
while length(s) < 2 do s := '0' + s;
fromdec := s;
end;
{
Функция, дополняющая строку до длины N нулями спереди
}
function wide_to(s: string; n: integer): string;
begin
while length(s) < n do s := '0' + s;
wide_to := s;
end;
{
Тестовые функции
}
const
{
s: string = 'A*/B+/A*/C*/D+B*/C*D';
}
s: string = 'A*/B+/A*C';
var
i, j, p, pp, vars_count: integer;
ch: char;
log_val, st, sub_s, params: string;
b_sum, b_mult: boolean;
begin
{ считаем количество переменных (vars_count) и заполняем список параметров (params) }
vars_count := 0; params := '';
for ch := 'A' to 'Z' do begin
if pos(ch, s) > 0 then begin
inc(vars_count);
params := params + ch;
end;
end;
{
Для построения таблицы истинности нужно перебрать все возможные значения
для всех параметров. Сделаем это простейшим способом: просто в цикле пройдем
от 0 до (2^vars_count) - 1, эти числа в двоичной системе счисления (дополненные
нулями до vars_count цифр) как раз и будут представлять собой комбинации True/False
на данной итерации цикла. Например:
0 = 000 (все параметры = False )
1 = 001 (gthdst 2 = False, третий = True)
...
7 = 111 (все параметры = True)
}
for i := 0 to pred(1 shl vars_count) do begin
log_val := wide_to(fromdec(i, 2), vars_count); { <--- текущая комбинация }
st := s + '+'; { Чтобы не портить исходную строку - работаем с копией }
b_sum := false; { эта переменная предназначена для хранения СУММЫ логических произведений }
repeat
p := pos('+', st); { <--- Есть ли еще знак суммы, другими словами - есть ли группа конъюнкций? }
if p > 0 then begin
sub_s := copy(st, 1, pred(p)); { <--- Да... Выделяем ее в переменную sub_s }
{
переменная предназначена для вычисления значения текущего произведения,
поэтому изначально равна True
}
b_mult := true;
{ Перебираем все параметры, смотрим, есть ли какой-то из них в текущей группе }
for j := 1 to length(params) do begin
pp := pos(params[j], sub_s);
if pp > 0 then begin { <--- Есть, pp хранит его позицию в строке }
{
далее возможны 2 варианта развития событий:
1. параметр присутствует с отрицанием (для этого позиция должна быть
БОЛЬШЕ 1, и предыдущим символом должен быть '/');
2. Параметр присутствует без отрицания...
}
if (pp > 1) and (sub_s[pp - 1] = '/') then begin { <--- Есть отрицание? }
{
Да, текущее логическое значение устанавливается в ОТРИЦАНИЕ
соответствующего значения из текущей комбинации параметров
}
b_mult := b_mult and not(log_val[j] = '1');
end
else begin
{ Нет, текущее значение берется без отрицания }
b_mult := b_mult and (log_val[j] = '1');
end;
end;
end;
delete(st, 1, p); { <--- удаляем обработанную группу конъюнкций из строки }
b_sum := b_sum or b_mult; { <--- дизъюнкция конъюнкций :) }
end
until p = 0; { повторять до тех пор, пока есть еще "+" в строке }
{ выводим результат: для (такой-то комбинации) значение функции равно (тому-то) }
writeln(log_val, ' = ', b_sum:5);
end;
end.