Примечание:
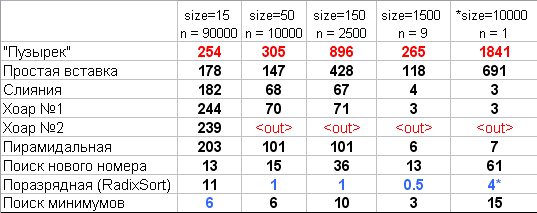
size: размер сортируемой последовательности
n: количество сортировок для замера времени
*: RadixSort в последнем тесте прогонялся при параметрах: size=21000; n=100
Сравнительная скорость работы некоторых нижеприведенных алгоритмов
сортировки:
Примечание:
size: размер сортируемой последовательности
n: количество сортировок для замера времени
*: RadixSort в последнем тесте прогонялся при параметрах: size=21000; n=100
1. Пузырьковая сортировка (простым выбором, линейная)
type
arrType = array[1 .. n] of integer;
procedure Bubble(var ar: arrType; n: integer);
var i, j, T: Integer;
begin
for i := 1 to n do
for j := n downto i+1 Do
if ar[Pred(j)] > ar[j] then begin { < }
T := ar[Pred(j)]; ar[Pred(j)] := ar[j]; ar[j] := T
end
end;
Еще один вариант реализации "пузырька", в котором нет необходимости заранее описывать тип arrType,
последовательность передается через открытый массив:
procedure Bubble(var ar: array of integer);
var
i, j: integer;
T: integer;
begin
for i := low(ar) to high(ar) do
for j := high(ar) downto i + 1 do begin
if ar[Pred(j)] > ar[j] then begin { < }
T := ar[Pred(j)]; ar[Pred(j)] := ar[j]; ar[j] := T
end
end;
end;
procedure BubbleSort(Mas: Pointer; Len: LongWord); asm dec Len @CycleExt: xor ebx, ebx mov ecx, Len mov esi, 0 @CycleIn: mov edi, Mas[esi] cmp edi, Mas[esi+4] jg @Exchange add esi, 4 loop @CycleIn jmp @Check @Exchange: mov ebx, Mas[esi+4] mov Mas[esi+4], edi mov Mas[esi], ebx add esi, 4 loop @CycleIn @Check: cmp ebx, 0 je @Exit jmp @CycleExt @Exit: end;
2. Сортировка простой вставкой
type
arrType = array[1 .. n] of integer;
procedure Insert(var ar: arrType; n: integer);
var
i, j: integer;
T: integer;
begin
for i := 1 to n do begin
T := ar[i];
j := Pred(i);
while (j >= 1) and (T < ar[j]) do begin
ar[Succ(j)] := ar[j]; Dec(j);
end;
ar[Succ(j)] := T;
end;
end;
Вариант с открытым массивом:
procedure Insert(var ar: array of integer);
var
i, j: integer;
T: integer;
begin
for i := low(ar) to high(ar) do begin
T := ar[i];
j := Pred(i);
while (j >= low(ar)) and (T < ar[j]) do begin
ar[Succ(j)] := ar[j]; Dec(j);
end;
ar[Succ(j)] := T;
end;
end;
Сложность этого алгоритма сортировки составляет О(n2)procedure merge(var ar: array of integer);
function ix(X: integer): integer;
begin ix := Pred(X) end;
procedure Slit(k, q: Integer);
type
TArr = array[1 .. maxint div sizeof(integer)] of integer;
var
m: integer;
i, j, T: integer;
D: ^TArr;
begin
GetMem(d, (high(ar) - low(ar) + 1) * sizeof(integer));
m := k + (q - k) div 2;
i := k; j := Succ(m); T := 1;
while (i <= m) and (j <= q) do begin
if ar[ix(j)] <= ar[ix(i)] then begin
D^[T] := ar[ix(i)]; Inc(i)
end
else begin
D^[T] := ar[ix(j)]; Inc(j)
end;
Inc(T)
end;
while i <= m do begin
D^[T] := ar[ix(i)]; Inc(i); Inc(T)
end;
while j <= q do begin
D^[T] := ar[ix(j)]; Inc(j); Inc(T)
end;
for i := 1 to Pred(T) do
ar[ix(Pred(k + i))] := D^[i];
freeMem(d, (high(ar) - low(ar) + 1) * sizeof(integer));
end;
procedure Sort(i, j: integer);
var T: integer;
begin
if i >= j then exit;
if j - i = 1 then begin
if ar[ix(i)] <= ar[ix(j)] then begin
T := ar[ix(i)]; ar[ix(i)] := ar[ix(j)]; ar[ix(j)] := T;
end
end
else begin
Sort(i, i + (j - i) div 2);
Sort(i + (j - i) div 2 + 1, j);
Slit(i, j)
end;
end;
begin
Sort(low(ar) + 1, high(ar) - low(ar) + 1);
end;Это улучшенный метод, основанный на обмене. При "пузырьковой"
сортировке производятся обмены элементов в соседних позициях. При пирамидальной сортировке
такой обмен совершается между элементами в позициях, жестко связанных друг с другом бинарным
деревом. Ниже будет рассмотрен алгоритм сортировки К. Хоара, использующий несколько иной
механизм выбора значений для обменов. Этот алгоритм называется сортировкой с разделением или быстрой
сортировкой. Она основана на том факте, что для достижения наибольшей эффективности желательно
производить обмены элементов на больших расстояниях.
Предположим, что даны N элементов массива, расположенные в обратном порядке. Их
можно рассортировать, выполнив всего N/2 обменов, если сначала поменять местами
самый левый и самый правый элементы и так далее, постепенно продвигаясь с двух
сторон к середине. Это возможно только, если мы знаем, что элементы расположены
строго в обратном порядке.
Рассмотрим следующий алгоритм: выберем случайным образом какой-то элемент
массива (назовем его x). Просмотрим массив, двигаясь слева направо, пока не
найдем элемент a[i]>x (сортируем по возрастанию), а затем просмотрим массив
справа налево, пока не найдем элемент a[j]<x. Далее, поменяем местами эти два
элемента a[i] и a[j] и продолжим этот процесс "просмотра с обменом", пока два
просмотра не встретятся где-то в середине массива.
После такого просмотра массив разделится на две части: левую - с элементами
меньшими (или равными) x, и правую - с элементами большими (или равными) x.
Итак, пусть a[k] (k=1,...,N) - одномерный массив, и x - какой-либо элемент из a.
Надо разбить "a" на две непустые непересекающиеся части а1 и а2 так, чтобы в a1
оказались элементы, не превосходящие x, а в а2 - не меньшие x.
Рассмотрим пример. Пусть в массиве a: <6, 23, 17, 8, 14, 25, 6, 3, 30, 7>
зафиксирован элемент x=14. Просматриваем массив a слева направо, пока не найдем
a[i]>x. Получаем a[2]=23. Далее, просматриваем a справа налево, пока не найдем
a[j]<x. Получаем a[10]=7. Меняем местами a[2] и a[10]. Продолжая этот процесс,
придем к массиву <6, 7, 3, 8, 6> <25, 14, 17, 30, 23>, разделенному на две
требуемые части a1, a2. Последние значения индексов таковы: i=6, j=5. Элементы
a[1],....,a[i-1] меньше или равны x=14, а элементы a[j+1],...,a[n] больше или
равны x. Следовательно,разделение массива произошло. Описанный алгоритм прост и
эффективен, так как сравниваемые переменные i, j и x можно хранить во время
просмотра в быстрых регистрах процессора. Наша конечная цель - не только
провести разделение на указанные части исходного массива элементов, но и
отсортировать его. Для этого нужно применить процесс разделения к получившимся
двум частям, затем к частям частей, и так далее до тех пор, пока каждая из
частей не будет состоять из одного единственного элемента. Эти действия
описываются следующей программой. Процедура Sort реализует разделение массива на
две части, и рекурсивно обращается сама к себе...
type
arrType = array[1 .. n] of integer;
{ первый вариант : }
procedure HoarFirst(var ar: arrType; n: integer);
procedure sort(m, l: integer);
var i, j, x, w: integer;
begin
i := m; j := l;
x := ar[(m+l) div 2];
repeat
while ar[i] < x do Inc(i);
while ar[j] > x do Dec(j);
if i <= j then begin
w := ar[i]; ar[i] := ar[j]; ar[j] := w;
Inc(i); Dec(j)
end
until i > j;
if m < j then Sort(m, j);
if i < l then Sort(i, l)
end;
begin
sort(1, n)
end;
{ второй вариант : }
procedure HoarSecond(var ar: arrType; n: integer);
procedure Sort(m, l: integer);
var i, j, x, w: integer;
begin
if m >= l then exit;
i := m; j := l;
x := ar[(m+l) div 2];
while i < j do
if ar[i] < x then Inc(i)
else if ar[j] > x then Dec(j)
else begin
w := ar[i]; ar[i] := ar[j]; ar[j] := w;
end;
Sort(m, Pred(j));
Sort(Succ(i),l);
end;
begin
Sort(1, n)
end;
Сложность O(n*logn), на некоторых тестах работает быстрее сортировки слияниями,
но на некоторых специально подобранных работает за O(n2).
5. Пирамидальная - турнирная - HeapSort сортировка
Type
arrType = Array[1 .. n] Of Integer;
Procedure HeapSort(Var ar: arrType; n: Integer);
Var
i, Left, Right: integer;
x: Integer;
Procedure sift;
Var i, j: Integer;
Begin
i := Left; j := 2*i; x := ar[i];
While j <= Right Do Begin
If j < Right Then
If ar[j] < ar[Succ(j)] Then Inc(j);
If x >= ar[j] Then Break;
ar[i] := ar[j];
i := j; j := 2 * i
End;
ar[i] := x
end;
Var T: Integer;
Begin
Left := Succ(n div 2); Right := n;
While Left > 1 Do Begin
Dec(Left); sift
End;
While Right > 1 Do Begin
T := ar[ Left ]; ar[ Left ] := ar[ Right ]; ar[ Right ] := T;
Dec(Right); sift
End
End;
6. Распределяющая сортировка - RadixSort - цифровая - поразрядная
for i := 0 to Pred(255) Do distr[i]:=0; for i := 0 to Pred(n) Do distr[source[i]] := distr[[i]] + 1;Для нашего примера будем иметь distr = ( 0, 0, 0, 0, 1, 1, 0, 3, 1, 1 ), то есть i-ый элемент distr[] - количество ключей со значением i.
index: array[0 .. 255] of integer; index[0]:=0; for i := 1 to Pred(255) Do index[i]=index[i-1]+distr[i-1];В index[i] мы поместили информацию о будущем количестве символов в отсортированном массиве до символа с ключом i.
for i := 0 to Pred(n) Do Begin
sorted[ index[ source[i] ] ]:=source[i];
{ попутно изменяем index уже вставленных символов, чтобы одинаковые ключи шли один за другим: }
index[ source[i] ] := index[ source[i] ] + 1;
End;
сначала они в сортируем по младшему на один беспорядке: разряду: выше: и еще раз: 523 523 523 088 153 153 235 153 088 554 153 235 554 235 554 523 235 088 088 554Hу вот мы и отсортировали за O ( k*n ) шагов. Если количество возможных различных ключей ненамного превышает общее их число, то 'поразрядная сортировка' оказывается гораздо быстрее даже 'быстрой сортировки'!
Const
n = 8;
Type
arrType = Array[0 .. Pred(n)] Of Byte;
Const
m = 256;
a: arrType = (44, 55, 12, 42, 94, 18, 6, 67);
Procedure RadixSort(Var source, sorted: arrType);
Type indexType = Array[0 .. Pred(m)] Of Byte;
Var
distr, index: indexType;
i: integer;
begin
fillchar(distr, sizeof(distr), 0);
for i := 0 to Pred(n) do
inc(distr[source[i]]);
index[0] := 0;
for i := 1 to Pred(m) do
index[i] := index[Pred(i)] + distr[Pred(i)];
for i := 0 to Pred(n) do begin
sorted[ index[source[i]] ] := source[i];
index[source[i]] := index[source[i]]+1;
end;
end;
var b: arrType;
begin
RadixSort(a, b);
end.
7. Пузырьковая сортировка с просеиванием
const n = 10;
var
x: array[1 .. n] of integer;
i, j, t: integer;
flagsort: boolean;
procedure bubble_P;
begin
repeat
flagsort := true;
for i := 1 to n - 1 do
if not(x[i]<=x[i + 1]) then begin
t := x[i];
x[i] := x[i + 1];
x[i + 1] := t;
j := i;
while (j > 1) and not(x[j-1] < =x[j]) do begin
t := x[j]; x[j] := x[j - 1]; x[j - 1] := t;
dec(j);
end;
flagsort := false;
end;
until flagsort;
end;
Добавлено: Тестировалось на массиве целых чисел (25000 элементов). Прирост скорости относительно простой пузырьковой сортировки - около 75%...
8. Древесная сортировка (TreeSort)
Const n = 8;
Type
TType = Integer;
arrType = Array[1 .. n] Of TType;
Const
a: arrType = (44, 55, 12, 42, 94, 18, 6, 67);
(* Сортировка с помощью бинарного дерева *)
Type
PTTree = ^TTree;
TTree = Record
a: TType;
left, right: PTTree;
End;
{ Добавление очередного элемента в дерево }
Function AddToTree(root: PTTree; nValue: TType): PTTree;
Begin
(* При отсутствии преемника создать новый элемент *)
If root = nil Then Begin
root := New(PTTree);
root^.a := nValue;
root^.left := nil;
root^.right := nil;
AddToTree := root; Exit
End;
If root^.a < nValue Then
root^.right := AddToTree(root^.right, nValue)
Else
root^.left := AddToTree(root^.left, nValue);
AddToTree := root
End;
(* Заполнение массива *)
Procedure TreeToArray(root: PTTree; Var a: arrType);
Const maxTwo: Integer = 1;
Begin
(* При отсутствии преемников рекурсия остановится *)
If root = nil Then Exit;
(* Левое поддерево *)
TreeToArray(root^.left, a);
a[maxTwo] := root^.a; Inc(maxTwo);
(* Правое поддерево *)
TreeToArray(root^.right, a);
Dispose(root)
End;
(* Собственно процедура сортировки *)
Procedure SortTree(Var a: arrType; n: Integer);
Var
root: PTTree;
i: Integer;
Begin
root := nil;
For i := 1 To n Do
root := AddToTree(root, a[i]);
TreeToArray(root, a)
End;
Var i: Integer;
Begin
WriteLn('До сортировки:');
For i := 1 To n Do Write(a[i]:4);
WriteLn;
SortTree(a, n);
WriteLn('После сортировки:');
For i := 1 To n Do Write(a[i]:4);
WriteLn
End.
9. Сортировка методом поиска нового номера
type
TArr = array[1..100] of integer;
var
mass1, NewMass : TArr;
n: integer;
{
n - размерность массива, mass1 - исходный массив,
NewMass - будет состоять из отсотртированных элементов массива mass1
}
procedure NewNSort(var mass, Nmass: TArr; size: integer);
var i, j, NewN: integer;
begin
for i := 1 to size do begin
NewN := 0;
for j := 1 to size do
if (mass[j]<mass[i]) or ((mass[j]=mass[i]) and (j<=i)) then inc(NewN);
Nmass[NewN] := mass[i];
end;
end;
Вызов:
NewNSort(mass1,NewMass,n);Массив NewMass будет состоять из элементов массива mass1, но уже отсортированных.
10. Метод последовательного поиска минимумов
type
TArr = array[1 .. 100] of integer;
var
mass1: TArr;
n : integer;
procedure NextMinSearchSort(var mass: TArr; size: integer);
var i, j, Nmin, temp: integer;
begin
for i := 1 to size - 1 do begin
nmin := i;
for j := i + 1 to size do
if mass[j] < mass[Nmin] then Nmin:=j;
temp := mass[i];
mass[i] := mass[Nmin];
mass[Nmin] := temp;
end;
end;
Вызов:
NextMinSearchSort(mass1, n);