Как построить график функции, заданной параметрически?

{$n+}
type
  tcurve = procedure(t: double;
           var x, y: double);
const
  scale = ... ; { масштаб изображения }

{
  Процедура для отрисовки точки кривой, 
  параметрическое представление которой задано функцией F
  при значении параметра = T
}
procedure set_point(t: double; f: tcurve);
var
  x, y: double;
begin
  f(t, x, y);
  putpixel( (getmaxx div 2) + trunc(scale * x),
            (getmaxy div 2) - trunc(scale * y), white );
end;

{
  Отрисовка кривой со значениями параметра,
  лежащими в интервале [start, finish] и шагом изменения параметра step
}
procedure draw_curve(start, finish, step: double;
          f: tcurve);
var t: double;
begin
  { отрисовываем оси координат }
  setcolor(green);
  line(0, getmaxy div 2, getmaxx, getmaxy div 2);
  line(getmaxx div 2, 0, getmaxx div 2, getmaxy);

  t := start; { начало интервала }

  { пока не вышли за границу интервала }
  while t <= finish do begin
    set_point(t, f);
    t := t + step; { наращиваем параметр }
  end;
end;

{ Пример использования: }
begin
  { Инициализируем графику... }

  draw_curve({начало интервала}, {конец интервала}, {шаг}, my_curve);
  readln;

  { Закрываем графику }
end.

{ Процедура должна компилироваться с директивой FAR }
procedure my_curve(t: double; var x, y: double); far;
begin
  x := ... ; { задание кривой }
  y := ... ;
end;

const
  a = 3;
  b = 9;
  L: double = 4;

  scale = 12;
  step = 0.005;

Исходник: curves.pas

Кривые 3-го порядка:

1. Полукубическая парабола:

   procedure semi_cubic(t: double; var x, y: double); far;
   begin
     x := sqr(t);
     y := a * sqr(t) * t;
   end;
   ...
   { Вызов: }
   draw_curve(-10, 10, step, semi_cubic);

   
2. Декартов лист

   procedure decart(t: double; var x, y: double); far;
   begin
     x := 3 * a * t / (1 + t * sqr(t));
     y := 3 * a * sqr(t) / (1 + t * sqr(t));
   end;
   ...
   { Вызов (двойной, т.к. в точке (-1) значение не определено): }
   draw_curve(-10, -1-step, step, decart);
   draw_curve(-1+step, 10, step, decart);

   
3. Циссоида:

   procedure cissoide(t: double; var x, y: double); far;
   begin
     x := a * sqr(t) / (1 + sqr(t));
     y := a * t * sqr(t) / (1 + sqr(t));
   end;
   ...
   { Вызов: }
   draw_curve(-10, 10, step, cissoide);

   
4. Строфоида:

   procedure strophoide(t: double; var x, y: double); far;
   begin
     x := a * (sqr(t) - 1) / (sqr(t) + 1);
     y := a * t * (sqr(t) - 1) / (sqr(t) + 1);
   end;
   ...
   { Вызов: }
   draw_curve(-10, 10, step, strophoide);

   

Кривые 4-го порядка:

1. Конхоида Никомеда:

   procedure conhoide(t: double; var x, y: double); far;
   begin
     x := a + L * cos(t);
     y := a * sin(t) / cos(t) + L * sin(t)
   end;
   ...
   { Вызов: }
   draw_curve(-pi/2+step, pi/2-step, step, conhoide); { правая ветвь }
   draw_curve(pi/2+step, 3*pi/2-step, step, conhoide); { левая ветвь }

   
2. "Улитка" Паскаля:

   procedure ulitka(t: double; var x, y: double); far;
   begin
     x := a * sqr(cos(t)) + l * cos(t);
     y := a * cos(t) * sin(t) + l * sin(t);
   end;
   ...
   { Вызов: }
   draw_curve(0, 2*pi-step, step, ulitka);

   
3. Кардиоида:

   procedure cardioide(t: double; var x, y: double); far;
   begin
     x := a * cos(t) * (1 + cos(t));
     y := a * sin(t) * (1 + cos(t));
   end;
   ...
   { Вызов: }
   draw_curve(0, 2*pi-step, step, cardioide);

   

Циклоиды, спирали, эвольвенты:

1. Циклоида:

   procedure cycloide(t: double; var x, y: double); far;
   begin
     x := a * (t - L * sin(t));
     y := a * (1 - L * cos(t));
   end;
   ...
   { Вызов: }
   cleardevice; L := 1; { Обычная }
   draw_curve(-10, 10, step, cycloide);
   readln;
   cleardevice; L := 0.3; { Укороченная }
   draw_curve(-10, 10, step, cycloide);
   readln;
   cleardevice; L := 3; { Удлиненная }
   draw_curve(-10, 10, step, cycloide);
   readln;

   
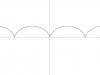
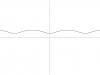
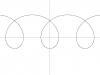
2. Эпициклоида:

   procedure epi_cycloide(t: double; var x, y: double); far;
   begin
     x := (a + B) * cos(t) - L * a * cos((a + B)*t / a);
     y := (a + B) * sin(t) - L * a * sin((a + B)*t / a);
   end;
   ...
   { Вызов: }
   cleardevice; L := 1; { Обычная }
   draw_curve(-10, 10, step, epi_cycloide);
   readln;
   cleardevice; L := 0.3; { Укороченная }
   draw_curve(-10, 10, step, epi_cycloide);
   readln;
   cleardevice; L := 3; { Удлиненная }
   draw_curve(-10, 10, step, epi_cycloide);
   readln;

   
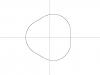
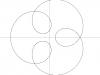
3. Гипоциклоида:

   procedure hypo_cycloide(t: double; var x, y: double); far;
   begin
     x := (b - a) * cos(t) + L * a * cos((b - a)*t / a);
     y := (b - a) * sin(t) - L * a * sin((b - a)*t / a);
   end;
   ...
   { Вызов: }
   cleardevice; L := 1; { Обычная }
   draw_curve(-10, 10, step, hypo_cycloide);
   readln;
   cleardevice; L := 0.3; { Укороченная }
   draw_curve(-10, 10, step, hypo_cycloide);
   readln;
   cleardevice; L := 3;  { Удлиненная }
   draw_curve(-10, 10, step, hypo_cycloide);
   readln;

   
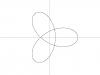
4. Гиперболическая спираль:

   procedure hyp_spiral(t: double; var x, y: double); far;
   begin
     x := a * cos(t)/t;
     y := a * sin(t)/t;
   end;
   ...
   { Вызов: }
   draw_curve(-10, -step, step, hyp_spiral); { ветка влево }
   draw_curve(step, 10, step, hyp_spiral); { ветка вправо }

   
5. Эвольвента (развертка) окружности:

   procedure evolventa(t: double; var x, y: double); far;
   begin
     x := a * cos(t) + a * t * sin(t);
     y := a * sin(t) - a * t * cos(t);
   end;
   ...
   { Вызов: }
   draw_curve(-10, 10, step, evolventa);