
Бинарные деревья (основные понятия)
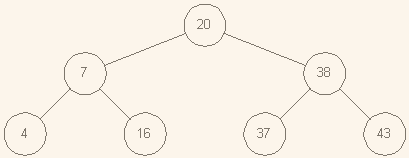
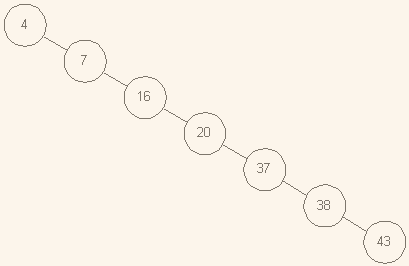
Операции над бинарными деревьями
type
T = Integer; { скрываем зависимость от конкретного типа данных }
TTree = ^TNode;
TNode = record
value: T;
Left, Right: TTree;
end;
Здесь поля Left и Right - это указатели на потомков данного узла, а поле value предназначено для хранения информации.
procedure Insert(var Root: TTree; X: T);
{ Дополнительная процедура, создающая и инициализирующая новый узел }
procedure CreateNode(var p: TTree; n: T);
begin
New(p);
p^.value := n;
p^.Left := nil;
p^.Right := nil
end;
begin
if Root = nil Then CreateNode(Root, X) { создаем новый узел дерева }
else
with Root^ do begin
if value < X then Insert(Right, X)
else
if value > X Then Insert(Left, X)
else
{ Действия, производимые в случае повторного
внесения элементов в дерево}
end;
end;Эта процедура добавляет элемент X к дереву, учитывая величину X. При этом создается новый узел дерева.function GetNode(Root: TTree): T;
begin
if Root = nil then WriteLn('Дерево - пусто!')
else
GetNode:=Root^.value
end;function Find(Root: TTree; X: T): TTree; begin if Root = nil then Find := nil else if X = Root^.value then Find := Root else if X < Root^.value then Find := Find(Root^.Left, X) else Find := Find(Root^.Right, X); end;
function DeleteMin(var Root: TTree): T;
var WasRoot: TTree;
begin
if Root^.Left = nil then begin
DeleteMin := Root^.value; { Результат функции }
WasRoot := Root; { Запоминаем узел для последующего удаления }
Root := Root^.Right; { продвигаемся дальше }
Dispose(WasRoot); { удаляем бывший корень }
end
else { узел Root имеет левого "сына" }
DeleteMin := DeleteMin(Root^.Left);
end;Теперь процедура Remove может быть реализована так:
procedure Remove(var Root: TTree; X: T);
var WasNext: TTree;
begin
if Root <> nil then
if X < Root^.value then Remove(Root^.Left, X)
else
if X > Root^.value then Remove(Root^.Right, X)
else
if (Root^.Left = nil) and (Root^.Right = nil) then begin
{ Нет "сыновей", удаляем узел, на который указывает Root }
Dispose(Root);
Root := nil
end
else
if Root^.Left = nil then begin
WasNext := Root^.Right;
Dispose(Root);
Root := WasNext;
end
else
if Root^.Right = nil then begin
WasNext := Root^.Left;
Dispose(Root);
Root := WasNext;
end
else { у удаляемого элемента есть оба "сына" }
Root^.value := DeleteMin(Root^.Right);
end;Procedure Delete(T: TTree); Begin If T = nil Then Exit; Delete(T^.Right); Delete(T^.Left); Dispose(T) End;
Таблица рекурсивных алгоритмов прохождения бинарного дерева
--------------------------------------------------------------------------------
Порядок прохождения
--------------------------------------------------------------------------------
Прямой | Симметричный | Концевой
--------------------------------------------------------------------------------
1. Корень поддерева |1. Левое поддерево |1. Левое поддерево
2. Левое поддерево |2. Корень поддерева |2. Правое поддерево
3. Правое поддерево |3. Правое поддерево |3. Корень поддерева
--------------------------------------------------------------------------------
procedure PrintByLevel(level: integer;
var items: array of TTree; count: integer);
var i, new_count: integer;
begin
if count <> 0 then begin
writeln('level = ', level);
new_count := 0;
for i := 0 to pred(count) do begin
write(items[i]^.value:4);
if items[i]^.left <> nil then begin
inc(new_count); items[count + new_count - 1] := items[i]^.left;
end;
if items[i]^.right <> nil then begin
inc(new_count); items[count + new_count - 1] := items[i]^.right;
end;
end;
writeln;
move(items[count], items[0], new_count*sizeof(TTree));
PrintByLevel(level + 1, items, new_count);
end;
end;
Вызывать процедуру надо вот так:
var
arr: array[0 .. pred(size)] of TTree; { <--- Здесь должно быть достаточно места для хранения }
begin
{ Заполнение дерева }
...
arr[0] := root;
PrintByLevel(0, arr, 1);
...
end.
Графическое представление бинарного дерева
Function Convert(X: T): String;так, чтобы она преобразовывала необходимый тип к строке...
Procedure LeafsCount(T: TTree; Var k: Integer);Процедуры обхода:
procedure PrintDown(level: integer; T: TTree); { Прямой порядок прохождения }
procedure PrintLex(level: integer; T: TTree); { Симметричный порядок прохождения }
procedure PrintUp(level: integer; T: TTree); { Концевой порядок прохождения }
Пример программы, использующей реализацию бинарного дерева:
uses TreeUnit;
const
size = 10;
iV: array[1 .. size] of Integer = (
1, 4, 8, 2, 7, 4, 3, 8, 9, 3
);
var
i: Integer;
myTree, wasfound: TTree;
begin
myTree := nil;
for i := 1 to size do begin
Insert(myTree, iv[i]);
PrintDown(0, myTree); WriteLn
end;
wasFound := Find(myTree, 7);
if wasFound <> nil then
WriteLn('x = ', GetNode(wasFound));
Remove(myTree, 7);
PrintDown(0, myTree);
end.
Нерекурсивная работа с бинарным деревом
Procedure AddIter(Var root: TTree; X: TType);
{ Функция, создающая новый лист дерева с заданным значением Data }
Function CreateNode(n: TType): TTree;
var p: TTree;
Begin
New(p);
p^.Data := n;
p^.Left := nil; p^.Right := nil;
CreateNode := p;
End;
var
parent, pwalk: TTree;
Begin
{
Если корень дерева - нулевой (только начали заполнять дерево, например),
то создаем новый элемент и запоминаем его, как корень
}
if root = nil then root := CreateNode(X)
else begin
{ Если дерево уже не пустое - тогда начинаем "прогулку" по нему... }
pWalk := root; { "гулять" начнем с корня }
while pWalk <> nil do begin { пока не добрались до пустого указателя - делаем следующее }
{ запоминаем текущий элемент, в качестве "родителя" его потомка }
parent := pWalk;
{
переходим в левую или правую ветвь в зависимости от соотношения величин
нового элемента и "текущего", которым мы "гуляем" по дереву
}
if X < pWalk^.data then pWalk := pWalk^.left
else pWalk := pWalk^.right
end;
{
Если мы здесь - значит, добрались до пустого указателя...
Вот теперь делаем то, для чего запоминали родителя текущего элемента:
опять же в зависимости от того, больше или меньше добавляемое значение,
чем значение "родителя", создаем новый элемент и запоминаем его в левой,
или правой ветке...
}
if X < parent^.data then parent^.left := CreateNode(X)
else parent^.right := CreateNode(X);
end;
End;