AVL деревья
В топике Бинарные деревья я
приводил пример вырожденного бинарного дерева. У такого дерева (фактически - списка узлов) есть явный недостаток: чем
больше бинарное дерево разбалансируется, тем больше замедляется скорость достура к данным, и если в идеально
сбалансированном дереве
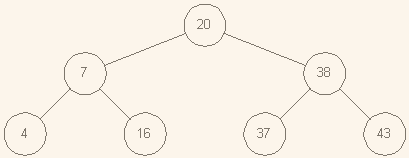
(рис 1)
доступ к узлу со значением 43 осуществляется за 2 шага, то в вырожденном его аналоге
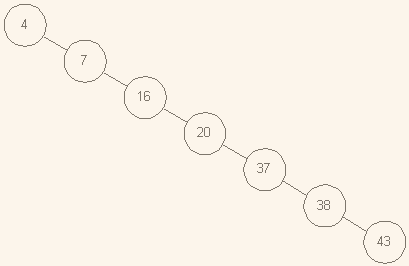
для этого потребуется - уже 6 шагов, то есть, фактически, нужно "пробежать" по всему списку, чтобы найти этот элемент.
Существует класс бинарных деревьев, которые обладают всеми преимуществами бинарных деревьев поиска, но при этом они не вырождаются.
Это - сбалансированные, или AVL (по фамилиям изобретателей данного алгоритма балансировки деревьев Adelson-Velski и Landis) деревья.
Несмотря на то, что AVL деревья не являются идеально сбалансированными, в них для каждого узла дерева высоты поддеревьев
различаются не более, чем на единицу. При этом общая высота дерева, содержащего N узлов, не превышает O(log2N), и AVL
дерево обеспечивает быстрый доступ к данным...
Теорию работы с AVL-деревьями можно найти здесь:
(Avl - деревья)
AVL-деревья
RSDN: AVL-деревья
Ниже приведена ООП-реализация AVL-дерева.
Несколько слов о реализации: само AVL дерево (AVLClass) унаследовано от класса двоичного дерева поиска (BSTClass):
type
BSTClass = object
{ ... двоичное дерево поиска ... }
end;
type
AVLClass = object(BSTClass)
{ ... AVL - дерево ... }
end;
То же самое касается и узлов: узлы дерева BSTClass имеют тип BSTNodeClass, а узлы AVL дерева наследуются от него:
type
BSTNodeClass = object
{ ... узлы дерева поиска ... }
end;
AVLNodeClass = object (BSTNodeClass)
{ ... узлы AVL - дерева ... }
end;
Тестовая программа для проверки работоспособности классов:
uses
Crt, avlnode, avltree;
Procedure Pause;
Begin
WriteLn('Для продолжения нажмите ENTER:');
Readln
End;
var
AVLTreeA, AVLTreeC: AVLClass;
_result: AVLNodePtr;
begin
WriteLn('Память перед использованием Avl: ', memavail);
AVLTreeA.Create;
AVLTreeA.Insert('F');
AVLTreeA.Insert('B');
AVLTreeA.Insert('W');
AVLTreeA.Insert('M');
AVLTreeA.Insert('E');
AVLTreeA.Insert('A');
AVLTreeA.Insert('C');
WriteLn('AVLTreeA на данный момент содержит:');
AVLTreeA.Print;
Pause;
{
Попытка разбалансировать Avl дерево... Добавляем элементы
Дерево должно самобалансироваться
}
AVLTreeA.Insert('X');
AVLTreeA.Insert('Y');
AVLTreeA.Insert('Z');
AVLTreeA.Insert('L');
AVLTreeA.Insert('K');
AVLTreeA.Insert('J');
AVLTreeA.Insert('I');
AVLTreeA.Insert('H');
AVLTreeA.Insert('N');
AVLTreeA.Insert('O');
AVLTreeA.Insert('R');
AVLTreeA.Insert('P');
AVLTreeA.Insert('Q');
WriteLn('AVLTreeA содержит:');
AVLTreeA.Print;
Pause;
_result := AVLNodePtr(AVLTreeA.Find('E'));
If _result = nil Then
WriteLn('Значение E не найдено в AVLTreeA (неверно).')
Else WriteLn('Значение E найдено в AVLTreeA (правильно).');
WriteLn('Число узлов в дереве AVLTreeA: ', AVLTreeA.NumItems);
Pause;
_result := AVLNodePtr(AVLTreeA.Find('D'));
If _result = nil Then
WriteLn('Значение D не найдено в AVLTreeA (правильно).')
Else WriteLn('Значение D найдено в AVLTreeA (неверно).');
Pause;
WriteLn('Попытка использования конструктора копирования для AVLClass:');
AVLTreeC.Copy(AVLTreeA);
WriteLn('AVLTreeC содержит:');
AVLTreeC.Print;
Pause;
WriteLn('Число узлов в дереве AVLTreeC: ', AVLTreeC.NumItems);
Pause;
_result := AVLNodePtr(AVLTreeC.Find('W'));
If _result = nil Then
WriteLn('Значение W не найдено в AVLTreeC (неверно).')
Else WriteLn('Значение W найдено в AVLTreeC (правильно).');
Pause;
{ Не забываем удалять деревья }
AVLTreeC.Destroy;
AVLTreeA.Destroy;
WriteLn('Память после использования Avl: ', memavail);
end.
Скачать проект, компилирующийся в TurboPascal 7.0:
avl_tp.rar
Для счастливых обладателей компилятора FPC выкладываю версию с переопределенными операторами, что позволит сделать
работу с AVL деревьями гораздо более удобной. К примеру, та же самая тестовая программа (даже с небольшими добавлениями)
будет иметь вид:
uses
avlnode, avltree;
Procedure Pause;
Begin
WriteLn('Press ENTER to continue:');
ReadLn;
End;
var
AVLTreeA, AVLTreeB, AVLTreeC: AVLClass;
p: AVLNodePtr;
begin
AVLTreeA.Create;
AvlTreeA := AVLTreeA + 'F' + 'B' + 'W' + 'M' + 'E' + 'A' + 'C';
WriteLn('AVLTreeA на данный момент содержит: ');
AVLTreeA.Print;
Pause;
{
Попытка разбалансировать Avl дерево... Добавляем элементы
Дерево должно самобалансироваться
}
AvlTreeA := AvlTreeA +
'X' + 'Y' + 'Z' + 'L' + 'K' + 'J' + 'I' +
'H' + 'N' + 'O' + 'R' + 'P' + 'Q';
WriteLn('AVLTreeA содержит:');
AVLTreeA.Print;
Pause;
p := AVLNodePtr(AVLTreeA.Find('E'));
If p = nil Then
WriteLn('Значение E не найдено в AVLTreeA (неверно).')
Else WriteLn('Значение E найдено в AVLTreeA (правильно).');
WriteLn('Число узлов в дереве AVLTreeA: ', AVLTreeA.NumItems);
Pause;
p := AVLNodePtr(AVLTreeA.Find('D'));
If p = nil Then
WriteLn('Значение D не найдено в AVLTreeA (правильно).')
Else WriteLn('Значение D найдено в AVLTreeA (неверно).');
Pause;
WriteLn('Попытка использования конструктора копирования для AVLClass:');
AVLTreeC.Create(AVLTreeA); { Перегрузка функций позволяет использовать то же имя }
WriteLn('AVLTreeC содержит:');
AVLTreeC.Print;
Pause;
WriteLn('Число узлов в дереве AVLTreeC: ', AVLTreeC.NumItems);
Pause;
p := AVLNodePtr(AVLTreeC.Find('W'));
If p = nil Then
WriteLn('Значение W не найдено в AVLTreeC (неверно).')
Else WriteLn('Значение W найдено в AVLTreeC (правильно).');
Pause;
{ Не забываем удалять деревья }
AVLTreeC.Destroy;
AVLTreeA.Destroy;
end.
Скачать проект для FPC (проверялось в 2.0.0 Target: win32)
avl_fpc.rar


